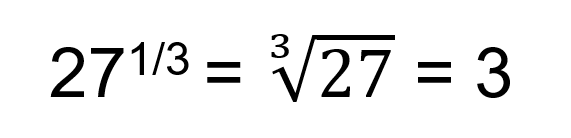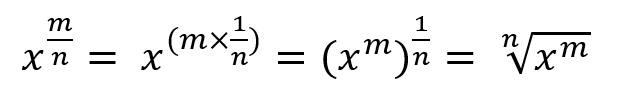Symbols are the main pillars of mathematics that connect one number to the other. There are many commonly used mathematical symbols like a plus(+), minus(-), multiplication (×), division (÷), and so on. One of these symbols, the exponent symbol, is the most important and common one. In this modern era, the importance of knowledge of exponent sign, its variants, usage in mathematics, and how to type it on different software and platforms can’t be denied.
An exponent refers to the number of times a number is multiplied by itself. The exponent sign was first introduced by Rene Descartes as early as the 17th century in his text named La Géométrie in which he told about its use and how to write. The exponents are the major parts of the algebraic expressions, binomial calculations, and math courses. An exponent symbol is a number or sign placed after and above some other number and symbol. The exponent symbol is also known as the power symbol because it is the power of the digit or number above it.
For example, bx means that x is the power of base “b”. It can also be pronounced like “b raised to the power of X. in this example the “b” is the base and “x” is the exponent.
Free Calculator to Find The Missing Exponents
Free Calculator to Find The Missing Base of an Exponent
There are several forms of exponents according to the situation and number being used as an exponent. Like addition, multiplication, division solving exponents demands a little bit more understanding of powers. Some of the major and most common calculations of exponents-related problems are discussed below.
When we talk about exponential expression, it means to write powers in a short way (short form) which indicate that how many times base is used as a factor.
For example:
81 can be written as 3 × 3 × 3 × 3, which states that 81 = 3 × 3 × 3 × 3 = 34 where 3 is a base and 4 is exponent
For example:
(32)5
Where 32 is base, 5 is an exponent.
Free Exponents Calculator Online
If the bases and exponents are same
If the bases and the exponents are the same then count such numbers and multiply them with one such base-exponent digit.
Example:
42 + 42 = 2 × 42 = 2 × 16 = 32
If the bases and exponents are different
The addition of exponent is also different for the different scenarios. If both the bases and exponents are different or the bases are same and exponents are different, the first resolves the exponents with their respective bases separately and then adds them up.
Example:
42 + 25= 4 × 4 + 2 × 2 × 2 × 2 × 2 = 16 + 32 = 48
42 + 43= 4 × 4 + 4 × 4 × 4 = 16 + 64 = 80
Free Online Calculator For Adding Exponents
Either the bases are the same or different
Subtraction of exponents is also not much difficult. First, you solve the numbers whether they are with the same bases or not, and then apply the simple subtraction to get the answer.
Example:
In this example first 2 raised to the power 3 is solved and then 2 raised to the power 2 is solved and then subtracted.
23 – 22 = 8 – 4 = 4
42 – 23 = 16 – 8 = 8
Free Online Calculator For Subtracting Exponents
There are several possibilities of multiplying exponents, some of which we will discuss here.
If the bases are the same
When we multiply the numbers having the same bases but different power then the exponents add up to each other.
Example:
42 × 44 = 42+4 = 46 = 4096
If the bases are different
If the bases are not the same then first resolve the exponent and then multiply the numbers.
Example:
32 × 43 = 9 × 64 = 576
Free Online Calculator For Multiplying Exponents
The division of the exponents is the opposite of the multiplication of the exponent.
If the bases are the same
In exponential division, if the bases are the same then the answer is also in the exponential form with the same base but the exponents subtracted with each other.
Example:
25 ÷ 23 = 25-3 = 22 = 4
In this only the exponents got subtracted without changing the base.
If the bases are different
If the bases and exponents are different then first resolve them separately and then perform the division.
Example:
43 ÷ 23 = 64 ÷ 8 = 8
Free Online Calculator For Dividing Exponents
In the negative exponent rule, the number having the negative exponent in the numerator is moved to the denominator as a whole. By doing this the negative exponent becomes the positive and then further calculations will be done.
Example:
(5)-2 = 1/52 = 1/(5 × 5) = 1/25 = 0.04
In this, a with negative exponent -2 become positive by moving to the denominator.
If the base is a fraction
In case if the base is a fraction and the exponent is negative then change the numerator of the base as a denominator and denominator into the numerator to make the exponent positive. In other words change the position of the base fraction.
Example:
(20/10)-7 = (10/20)7
Calculate Negative Exponents Online
If the bases and exponents are the same
Fractional exponents are also called rational or radical exponents. In this situation, if the exponent is in the form of a fraction like 1/2, 2/3, ¾, and so on. If the bases and exponents are the same then first resole the fraction and make a real number exponent and then do further calculations.
Example:
91/2 × 91/2 = 9(1/2+1/2) = 9(1) = 9
In this example, we first take the LCM of the same fractional exponents and after doing this we get the whole number fraction. By doing this we solve the fractional exponents.
If the fractional exponent is x1/n
The general rule in solving x1/n is that simply take the root with the number in the denominator of the fraction.
Example
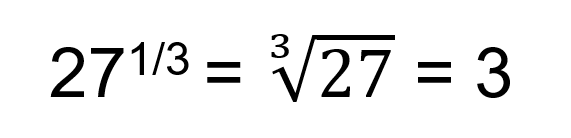
In this 1/3 becomes the cube root of the base. This is called the nth root rule.
If the exponent is in xm/n form
If both the numerator and denominator of the exponent are not different numbers then split the exponent into two parts, one is the real number(m) and the other into fraction form(1/n).
Example:
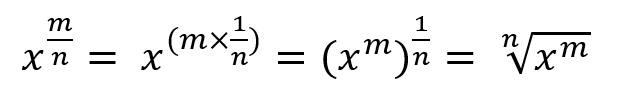
We can solve such exponents in this way.
In this modern age, almost all the writings and calculations are done either on the computer or other software as compared to writing on hard copy. So if one wants to deal with mathematics on these versatile platforms one should know how to type these symbols on them.